SageMath | Русскоязычная документация по Ubuntu

Содержание

SageMath

Программный пакет «SageMath» (см. Официальный сайт) позиционируется разработчиками как открытая альтернатива известным математическим программам, таким как «Matlab», «Maple» и др. И хотя не всё реализовано, но программа уже применима для научной деятельности. «SageMath» написана на «Python» и объединяет в себе программные математические библиотеки: «SciPy», «NumPy», «Matplotlib» (см. Matplotlib Gallery) и другие (см. Содержащиеся в Sage программные пакеты).

Установка

Программа «SageMath» доступна в виде исходных кодов или готовых сборок для «Unix»-подобных ОС (см. Download). Запуск под управлением ОС семейства «Windows» требует применения виртуализации.

Для удобства работы можно воспользоваться PPA-репозиторием ppa:aims/sagemath, добавить который в список источников ПО можно командами в терминале

sudo apt-add-repository -y ppa:aims/sagemath
sudo apt-get update
sudo apt-get install sagemath-upstream-binary

Запуск

«SageMath» может работать в двух режимах:

Консольный
Веб-интерфейс «Notebook»

Запустить «SageMath» можно командой в терминале

sage

или, что по сути тоже самое

sagemath

Первый запуск займет некоторое время, так как программа подстраивается под новую структуру каталогов, этот процесс нельзя перерывать

Через некоторое время будет выведено приглашения для работы:

sage:

теперь можно работать в консольном режиме.

Если же требуется запустить веб-интерфейс «Notebook», то в консоли «SageMath» необходимо ввести команду

notebook()

При этом запустится веб-браузер по адресу localhost:8080

Использование

Практические примеры разной сложности доступны в документации к самому программному пакету «SageMath» (см. Tutorial) и к входящим в него библиотекам. Непосредственную консультацию по конкретному вопросу можно получить в AskSage.

Консольный режим и веб-интерфейс поддерживают автодополнение команд и переменных (наберите начало команды, а затем нажмите Tab). Получение краткой информации о команде возможно с использование символа «?», например,

notebook?

При этом откроется консольный интерфейс просмотра документации, выйти из него можно нажав кнопку Q

Вывод графиков

Отдельной проблемой любой научной работы является представление результатов. По-умолчанию, «SageMath» предоставляет простую отрисовку графиков. Для более сложных графиков целесообразно воспользоваться библиотекой «Matplotlib» (см. Matplotlib Gallery). Хотя, возможно, придется затем обработать их в «Inkscape» для исправления незначительных проблем. Пример получения графиков в векторном формате SVG доступен в архиве, его следует скачать, распаковать, открыть папку в терминале, запустить «SageMath» и в её консоли ввести

load Main.sage

или просто в консоли «BASH» ввести

echo "load Main.sage" | sage

в таком случае «SageMath» закроется по завершении, что удобно для применения в скриптах. В подкаталоге «SVG» должны появится файлы графиков (из-за наличия недоработок в «librsvg» изображения следует просматривать в «Inkscape» или «Firefox»), например, такие

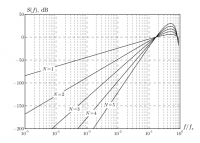
Используя код из этих примеров можно получить свои графики.

Ещё один пример

Цель – получение такого графика Выполнить программу можно в веб-интерфейсе «SageMath» notebook(). Создайте новый лист («New Worksheet»), придумайте ему имя. Нажмите кнопку «Edit» для перехода в текстовый режим, выделите всё и замените на приведенный ниже код

{{{id=5|
# Сброс
reset()
///
}}}
 
{{{id=3|
# Добавляем переменные для аналитических расчётов
var('p, T, omega, a, b, K1')
///
}}}
 
{{{id=1|
# Задаём некие численные переменные
K = 80.0
vK1 = 80.0
va = 7 # это считается целым числом, что-бы сделать его дробным следует писать "7.0" или "7."
vb = 5
vT = 0.1
///
}}}
 
{{{id=2|
# Некое уравнение
W1 = K1 / ((p + a)*(p + b))
///
}}}
 
{{{id=6|
# Вывод в понятном для человека виде
show(W1)
///
}}}
 
{{{id=7|
# Вычисляем значение аналитической функции в точке (параметры указаны явно)
W1 = W1(a = va, b = vb)
///
}}}
 
{{{id=8|
show(W1);
///
}}}
 
{{{id=9|
# Ещё аналитические вычисления
S1 = (1 - e^(-p*T)) / p
S2 = S1 * W1
///
}}}
 
{{{id=10|
show(S1); show(S2);
///
}}}
 
{{{id=11|
# Знаменатель из выражения выше
A = S2.denominator();
show(A);
///
}}}
 
{{{id=21|
# Раскрываем скобки и берём производную по p
Ad = A.expand().diff(p)
///
}}}
 
{{{id=14|
show(Ad)
///
}}}
 
{{{id=16|
# Числитель из S2
B = S2.numerator();
show(B);
///
}}}
 
{{{id=17|
# Находим корни уравнения A = 0 с указанием дополнительных параметров отображения результата для удобства
pz = solve(A == 0, p, solution_dict = True)
///
}}}
 
{{{id=18|
show(pz)
///
}}}
 
{{{id=19|
# Представляем корни в виде простого массива
pz = [s[p] for s in pz];
show(pz);
///
}}}
 
{{{id=20|
# Построение более сложного уравнения с использованием цикла
s = 0
l = len(pz) # длина массива pz
for i in range(0, l): # цикл
	s = s + (B(p = pz[i]) / Ad(p = pz[i]))*(e^(p*T) / (e^(p*T) - e^(pz[i]*T)))
show(s) # вывод в красивой форме
///
}}}
 
{{{id=22|
# Более сложное выражение на основе имеющихся
wl = s / (1 + s);
show(wl)
///
}}}
 
{{{id=24|
# Упрощаем используя все известные приёмы
wl = wl.simplify_full();
show(wl);
///
}}}
 
{{{id=25|
# Знаменатель
A = wl.denominator();
show(A);
///
}}}
 
{{{id=26|
# Значение в точке
A = A(K1 = vK1, T = vT);
show(A);
///
}}}
 
{{{id=27|
# Замена переменной p на jω, где j это мнимая единица, записывается как 1j без знака умножения
A = A(p = 1j*omega);
show(A);
///
}}}
 
{{{id=28|
# Действительная часть с упрощением выражения
Are = A.real().simplify_full();
show(Are);
# Мнимая часть с упрощением выражения
Aim = A.imag().simplify_full();
show(Aim);
///
}}}
 
{{{id=29|
# Подготовка к выводу графика
omega2 = pi/vT;
///
}}}
 
{{{id=30|
# Подключение библиотеки которая включает в себя другие полезные библиотеки, например, matplotlib для выводу графиков
# Хотя её можно подключить и отдельно
import pylab
///
}}}
 
{{{id=31|
# Строим массивы численных данных для графиков
aw = pylab.linspace(0, 100, 1001) # линейный массив от 0 до 100 с 1001-отсчётом
aRe = pylab.array([]) # пустой массив
aRe = pylab.resize(aRe, pylab.size(aw)) # меняем размер
aIm = pylab.array([])
aIm = pylab.resize(aIm, pylab.size(aw))
for i in range(0, pylab.size(aw)):
    aRe[i] = Are(omega = aw[i])
    aIm[i] = Aim(omega = aw[i])
 
aw2 = pylab.linspace(0, 60, 11)
aRe2 = pylab.array([])
aRe2 = pylab.resize(aRe2, pylab.size(aw2))
aIm2 = pylab.array([])
aIm2 = pylab.resize(aIm2, pylab.size(aw2))
for i in range(0, pylab.size(aw2)):
    aRe2[i] = Are(omega = aw2[i])
    aIm2[i] = Aim(omega = aw2[i])
 
aw3 = pylab.linspace(0, omega2, 1001)
aRe3 = pylab.array([])
aRe3 = pylab.resize(aRe3, pylab.size(aw3))
aIm3 = pylab.array([])
aIm3 = pylab.resize(aIm3, pylab.size(aw3))
for i in range(0, pylab.size(aw3)):
    aRe3[i] = Are(omega = aw3[i])
    aIm3[i] = Aim(omega = aw3[i])
///
}}}
 
{{{id=33|
Name = 'image' # текстовая строка для названия рисунка
Font1 = pylab.matplotlib.font_manager.FontProperties(family = 'CMU Serif', size = 12) # шрифт
Fig = pylab.figure()	# новый рисунок
Fig.set_size_inches([10., 10.])	# размер рисунка в дюймах
Fig.hold(True) # не стирать имеющиеся графики с рисунка при выводе новых
#-------------------------------------------------------------------------------------------------
Axis = pylab.subplot(111)	# создаём поле для рисования графика
Fig.add_subplot(Axis)
# Шрифт для меток осей координат по X и Y
pylab.xticks(fontproperties = Font1)
pylab.yticks(fontproperties = Font1)
#Axis.grid(b = True, which='major', linestyle = 'none')
Axis.set_axis_bgcolor([1., 1., 1.]) # цвет фона графика RGB (1, 1, 1) = белый
Axis.set_frame_on(True) # обрамление
Axis.set_title('', fontproperties = Font1) # шрифт заголовка
# Место положения названия оси координат в относительных единицах по X
Axis.xaxis.set_label_coords(1.02, 0.02)
Axis.yaxis.set_label_coords(0.02, 1.02)
# Координатная сетка (тип сетки, тип линии, ширина линии, цвет)
# большая
Axis.grid(which='major', linestyle = '--', linewidth=0.5, color=[0., 0., 0.])
# мелкая
Axis.grid(which='minor', linestyle=':', linewidth=1., color=[0., 0., 0.])
# Названия осей
Axis.set_xlabel('X',
	fontproperties = Font1,
	rotation='horizontal',
	weight='normal',
	size='large')
Axis.set_ylabel('Y',
	fontproperties = Font1,
	rotation='horizontal',
	weight='normal',
	size='large')
# Штрихи на осях
Axis.xaxis.set_ticks_position('bottom') # внизу на X
Axis.yaxis.set_ticks_position('left') # и слева на Y
# Масштаб осей (linear - линейный, log - логарифмический)
Axis.set_xscale('linear')
Axis.set_yscale('linear')
# Границы осей по значениям
#Axis.set_xlim(0, 0.9)
#Axis.set_ylim(0, 1.2)
#-------------------------------------------------------------------------------------------------
# Рисуем кривые на графике
Curve = Axis.plot(aRe, aIm, # данные, X и Y в виде массивов
	linestyle = '-', # тип линии
	linewidth = 1, # толщина линии
	fillstyle = 'full', # заполнение
	color = [0., 0., 0.], # цвет линии
	marker = 'None', # маркер для точки
	markeredgecolor = [0., 0., 0.], # цвет границы маркера
	markeredgewidth = 0.5, # толщина границы маркера
	markerfacecolor = [0., 0., 0.], # цвет заливки маркера
	markerfacecoloralt = [0., 0., 0.], # дополнительный цвет
	markersize = 6, # размер маркера
	dash_joinstyle = 'round' # тип соединения линий
	)[0]; # Axis.plot позволяет рисовать сразу много кривых и выдаёт их идентификаторы как массив, нам нужен 0-й элемент
Curve = Axis.plot(aRe2, aIm2,
	linestyle = 'None',
	linewidth = 1,
	fillstyle = 'full',
	color = [0., 0., 0.],
	marker = 'o',
	markeredgecolor = [0., 0., 0.],
	markeredgewidth = 0.5,
	markerfacecolor = [0., 0., 0.],
	markerfacecoloralt = [0., 0., 0.],
	markersize = 6,
	dash_joinstyle = 'round'
	)[0];
Curve = Axis.plot(aRe3, aIm3,
	linestyle = '-',
	linewidth = 3,
	fillstyle = 'full',
	color = [0., 0., 0.],
	marker = 'None',
	markeredgecolor = [0., 0., 0.],
	markeredgewidth = 0.5,
	markerfacecolor = [0., 0., 0.],
	markerfacecoloralt = [0., 0., 0.],
	markersize = 6,
	dash_joinstyle = 'round'
	)[0];
Curve = Axis.plot((Are(omega = omega2)).n(), (Aim(omega = omega2)).n(),
	linestyle = 'None',
	linewidth = 3,
	fillstyle = 'full',
	color = [0., 0., 0.],
	marker = 's',
	markeredgecolor = [0., 0., 0.],
	markeredgewidth = 0.5,
	markerfacecolor = [0., 0., 0.],
	markerfacecoloralt = [0., 0., 0.],
	markersize = 6,
	dash_joinstyle = 'round'
	)[0];
#-------------------------------------------------------------------------------------------------
# Хитрим для отображения меток посреди графика
dx = (Axis.get_xlim()[1] - Axis.get_xlim()[0])
dy = (Axis.get_ylim()[1] - Axis.get_ylim()[0])
bbox_props = dict(boxstyle="round4", fc=[1.0, 1.0, 1.0], ec=[1.0, 1.0, 1.0], alpha=1.0)
for i in range(0, pylab.size(aw2)):
    Axis.text(aRe2[i]+dx*0.001, aIm2[i]+dy*0.02, '$\omega = ' + latex(aw2[i]) + '$', ha="center", va="bottom", size=12, bbox=bbox_props)
 
Axis.text((Are(omega = omega2)).n()+dx*0.001, (Aim(omega = omega2)).n()+dy*0.02, '$\omega = \pi / T$', ha="center", va="bottom", size=12, bbox=bbox_props)
#-------------------------------------------------------------------------------------------------
# Задаём имя файла и сохраняем график в него
FileName = os.path.join(Name + '.svg');
Fig.savefig(FileName, dpi = 96)
///
}}}
 
{{{id=35|
 
///
}}}

Нажмите «Save changes» и затем в списке «Action» выберите «Evaluate All», подождите пока всё завершится. Внизу должен появится график. Он имеет дефект, но это поправимо средствами «Inkscape».

Если Вы хотите выполнить этот код в терминале «SageMath», то ниже приведен тот же код что и выше, только без синтаксиса веб-интерфейса и без команд show(), выполнение которых в терминале приведёт к генерации *.dvi файла для каждого выражения, а это негативно скажется на быстроте работы ОС.

# Очиска консоли
os.system('clear')
print('--Begin-----------------------------------------------------------------------')
 
# Сброс
reset()
 
# Добавляем переменные для аналитических расчётов
var('p, T, omega, a, b, K1')
 
# Задаём некие численные переменные
K = 80.0
vK1 = 80.0
va = 7 # это считается целым числом, что-бы сделать его дробным следует писать "7.0" или "7."
vb = 5
vT = 0.1
 
# Некое уравнение
W1 = K1 / ((p + a)*(p + b))
 
# Вычисляем значение аналитической функции в точке (параметры указаны явно)
W1 = W1(a = va, b = vb)
 
# Ещё аналитические вычисления
S1 = (1 - e^(-p*T)) / p
S2 = S1 * W1
 
# Знаменатель из выражения выше
A = S2.denominator();
 
# Раскрываем скобки и берём производную по p
Ad = A.expand().diff(p)
 
# Числитель из S2
B = S2.numerator();
 
# Находим корни уравнения A = 0 с указанием дополнительных параметров отображения результата для удобства
pz = solve(A == 0, p, solution_dict = True)
 
# Представляем корни в виде простого массива
pz = [s[p] for s in pz];
 
# Построение более сложного уравнения с использованием цикла
s = 0
l = len(pz) # длина массива pz
for i in range(0, l): # цикл
	s = s + (B(p = pz[i]) / Ad(p = pz[i]))*(e^(p*T) / (e^(p*T) - e^(pz[i]*T)))
 
# Более сложное выражение на основе имеющихся
wl = s / (1 + s);
 
# Упрощаем используя все известные приёмы
wl = wl.simplify_full();
 
# Знаменатель
A = wl.denominator();
 
# Значение в точке
A = A(K1 = vK1, T = vT);
 
# Замена переменной p на jω, где j это мнимая единица, записывается как 1j без знака умножения
A = A(p = 1j*omega);
 
# Действительная часть с упрощением выражения
Are = A.real().simplify_full();
 
# Мнимая часть с упрощением выражения
Aim = A.imag().simplify_full();
 
# Подготовка к выводу графика
omega2 = pi/vT;
 
# Подключение библиотеки которая включает в себя другие полезные библиотеки, например, matplotlib для выводу графиков
# Хотя её можно подключить и отдельно
import pylab
#------------------------------------------------------
# Строим массивы численных данных для графиков
aw = pylab.linspace(0, 100, 1001) # линейный массив от 0 до 100 с 1001-отсчётом
aRe = pylab.array([]) # пустой массив
aRe = pylab.resize(aRe, pylab.size(aw)) # меняем размер
aIm = pylab.array([])
aIm = pylab.resize(aIm, pylab.size(aw))
for i in range(0, pylab.size(aw)):
    aRe[i] = Are(omega = aw[i])
    aIm[i] = Aim(omega = aw[i])
 
aw2 = pylab.linspace(0, 60, 11)
aRe2 = pylab.array([])
aRe2 = pylab.resize(aRe2, pylab.size(aw2))
aIm2 = pylab.array([])
aIm2 = pylab.resize(aIm2, pylab.size(aw2))
for i in range(0, pylab.size(aw2)):
    aRe2[i] = Are(omega = aw2[i])
    aIm2[i] = Aim(omega = aw2[i])
 
aw3 = pylab.linspace(0, omega2, 1001)
aRe3 = pylab.array([])
aRe3 = pylab.resize(aRe3, pylab.size(aw3))
aIm3 = pylab.array([])
aIm3 = pylab.resize(aIm3, pylab.size(aw3))
for i in range(0, pylab.size(aw3)):
    aRe3[i] = Are(omega = aw3[i])
    aIm3[i] = Aim(omega = aw3[i])
#-------------------------------------------------------------------------------------------------
Name = 'O_o'
Font1 = pylab.matplotlib.font_manager.FontProperties(family = 'CMU Serif', size = 12) # шрифт
Fig = pylab.figure()	# новый рисунок
Fig.set_size_inches([10., 10.])	# размер рисунка в дюймах
Fig.hold(True) # не стирать имеющиеся графики с рисунка при выводе новых
#-------------------------------------------------------------------------------------------------
Axis = pylab.subplot(111)	# создаём оси - поле для рисования графика
Fig.add_subplot(Axis)
# Шрифт для меток осей координат по X и Y
pylab.xticks(fontproperties = Font1)
pylab.yticks(fontproperties = Font1)
#Axis.grid(b = True, which='major', linestyle = 'none')
Axis.set_axis_bgcolor([1., 1., 1.]) # цвет фона графика RGB (1, 1, 1) = белый
Axis.set_frame_on(True) # обрамление
Axis.set_title('', fontproperties = Font1) # шрифт заголовка
# Место положения названия оси координат в относительных единицах по X
Axis.xaxis.set_label_coords(1.02, 0.02)
Axis.yaxis.set_label_coords(0.02, 1.02)
# Координатная сетка (тип сетки, тип линии, ширина линии, цвет)
# большая
Axis.grid(which='major', linestyle = '--', linewidth=0.5, color=[0., 0., 0.])
# мелкая
Axis.grid(which='minor', linestyle=':', linewidth=1., color=[0., 0., 0.])
# Названия осей
Axis.set_xlabel('X',
	fontproperties = Font1,
	rotation='horizontal',
	weight='normal',
	size='large')
Axis.set_ylabel('Y',
	fontproperties = Font1,
	rotation='horizontal',
	weight='normal',
	size='large')
# Штрихи на осях
Axis.xaxis.set_ticks_position('bottom') # внизу на X
Axis.yaxis.set_ticks_position('left') # и слева на Y
# Масштаб осей (linear - линейный, log - логарифмический)
Axis.set_xscale('linear')
Axis.set_yscale('linear')
# Границы осей по значениям
#Axis.set_xlim(0, 0.9)
#Axis.set_ylim(0, 1.2)
#-------------------------------------------------------------------------------------------------
Curve = Axis.plot(aRe, aIm,
	linestyle = '-',
	linewidth = 1,
	fillstyle = 'full',
	color = [0., 0., 0.],
	marker = 'None',
	markeredgecolor = [0., 0., 0.],
	markeredgewidth = 0.5,
	markerfacecolor = [0., 0., 0.],
	markerfacecoloralt = [0., 0., 0.],
	markersize = 6,
	dash_joinstyle = 'round'
	)[0];
Curve = Axis.plot(aRe2, aIm2,
	linestyle = 'None',
	linewidth = 1,
	fillstyle = 'full',
	color = [0., 0., 0.],
	marker = 'o',
	markeredgecolor = [0., 0., 0.],
	markeredgewidth = 0.5,
	markerfacecolor = [0., 0., 0.],
	markerfacecoloralt = [0., 0., 0.],
	markersize = 6,
	dash_joinstyle = 'round'
	)[0];
Curve = Axis.plot(aRe3, aIm3,
	linestyle = '-',
	linewidth = 3,
	fillstyle = 'full',
	color = [0., 0., 0.],
	marker = 'None',
	markeredgecolor = [0., 0., 0.],
	markeredgewidth = 0.5,
	markerfacecolor = [0., 0., 0.],
	markerfacecoloralt = [0., 0., 0.],
	markersize = 6,
	dash_joinstyle = 'round'
	)[0];
Curve = Axis.plot((Are(omega = omega2)).n(), (Aim(omega = omega2)).n(),
	linestyle = 'None',
	linewidth = 3,
	fillstyle = 'full',
	color = [0., 0., 0.],
	marker = 's',
	markeredgecolor = [0., 0., 0.],
	markeredgewidth = 0.5,
	markerfacecolor = [0., 0., 0.],
	markerfacecoloralt = [0., 0., 0.],
	markersize = 6,
	dash_joinstyle = 'round'
	)[0];
#-------------------------------------------------------------------------------------------------
dx = (Axis.get_xlim()[1] - Axis.get_xlim()[0])
dy = (Axis.get_ylim()[1] - Axis.get_ylim()[0])
bbox_props = dict(boxstyle="round4", fc=[1.0, 1.0, 1.0], ec=[1.0, 1.0, 1.0], alpha=1.0)
for i in range(0, pylab.size(aw2)):
    Axis.text(aRe2[i]+dx*0.001, aIm2[i]+dy*0.02, '$\omega = ' + latex(aw2[i]) + '$', ha="center", va="bottom", size=12, bbox=bbox_props)
 
Axis.text((Are(omega = omega2)).n()+dx*0.001, (Aim(omega = omega2)).n()+dy*0.02, '$\omega = \pi / T$', ha="center", va="bottom", size=12, bbox=bbox_props)
#-------------------------------------------------------------------------------------------------
FileName = os.path.join(Name + '.svg');
Fig.savefig(FileName, dpi = 96)
print('[ OK ]\n')
print('--End-------------------------------------------------------------------------')

Ссылки

Примеры использования библиотеки «Matplotlib» Matplotlib Gallery
Официальный сайт SageMath
Ответы на попросы AskSage

sagemath